Discounted cash flow (DCF) & Net present value (NPV) AO3, AO4
Discounted cash flow (DCF)Discounted cash flow (DCF) analysis is a method of valuing a project, company, or asset using the concepts of the time value of money. DCF is used to calculate the value of future cash flows in terms of an equivalent value today. All future cash flows are estimated and discounted to give their present values (PVs). This allows valid comparison with the cost of a project which is in today's value (present value). |
 What is the time value of money?
What is the time value of money?
Intuitively, would you prefer to be given $100 today or a promise that you will receive $100 in 1 year's time?
Most people would prefer the $100 right now, So you can see
money received today is more valuable to you than money received in a
year's time. Time reduces the value of money
More technically, when you were younger, you probably looked at compound interest in mathematics and were asked some simple questions such as,
If you had $100 and put it in the bank at 10% interest how much would you have at the end of:
Year 1?
Year 2?
Year 3? and so on...
The answers are:
Year 1 $110 ($100 + $100 x 10 per cent) or ($100 x 1.1).
Year 2 $121 ($110 + $110 x 10 per cent) or ($110 x 1.1).
Year 3 $133.1 ($121 + $121 x 10 per cent) or ($121 x 1.1).
N.B. Multiplying by 1.1 is the same as working out 110%.
Why is it called compound interest? The reason is that you will get 10% interest on your original $100 deposit (the principal) plus you also get 10% interest on any previous interest. So in the case of year 2 to year 3, you will receive 10% on your original $100 (which is $10) plus an additional 10% on your $21 interest (which is $2.1). So in total you receive $12.1 interest. Add that to your $121 and you get $133.1.
Compound interest
Compound interest is interest which is calculated not only on the initial principal, but also the accumulated interest of prior periods. Compound interest differs from simple interest in that simple interest is calculated solely as a percentage of the principal sum.
Therefore, it can be asked what $110 earned in one year's time is worth today (the Present Value or PV) if the interest rate is 10%. One way of thinking of this is reverse compound interest. The answer is obviously $100 as this could have been invested a year ago at 10 per cent to earn $10 in interest giving $110. Therefore $100 is worth the same as $110 received in a year's time or $121 received in two years' time. This indicates the time value of money
Discounted Cash Flow (DCF) deals with the two problems of interest rates and time. The return on an investment project is always in the future, usually over a period of several years. Money earned or paid in the future is worth less today, because of the concept of reversecompound interest:
We have already seen that, $100 is worth the same as $110 received in a year's time or $121 received in two years' time. This indicates the time value of money. So the Present Value or PV of $110 received in a year's time is $100 as this could have been invested today at 10 per cent to earn $10 in interest giving $110 at the end of the year. $100 today is therefore exactly the same in financial terms as $110 received at the end of the year. By now you should be getting the point!
Therefore, if a business wishes to compare two possible investments, which deliver different returns in the future, it is impossible to compare the relative merits unless the business can compare 'like with like'. To achieve this, all future returns must be converted into present values (PV). This can be achieved by discounting future returns.
To evaluate the worth of an investment we will then need to calculate the Net Present Value:
Net Present Value
The Net Present Value (NPV) of a project is the return on the investment (the sum of the discounted cash flows) less the cost of the investment.
If the NPV is larger than the initial cost (positive NPV), then the firm will see a return on its money. If it is less than the initial cost (negative NPV) then the project is not worth pursuing.

An investment project costing $100,000 yields an expected stream of income over a three year period of:
Year 1 - $30,000
Year 2 - $40,000
Year 3 - $50,000
If the interest rate is 10%, the discount values (present values) can be calculated using the technique below:
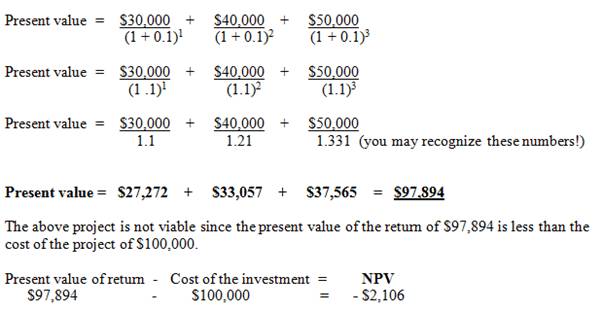
The firm will be losing money on the investment (a negative NPV), so should not undertake it.
Hold up - don't worry - read on
Fortunately, it is not necessary to carry out these discount factor calculations as tables of discounted values at different interest rates can be used and should be included with the examination paper (unless the examination board forgets to do so, which can happen!). The example above shows you how the discount factors are worked out.
The extract of a table below shows the present value of $1 receivable for a 6 year period at an interest rate of 5% per cent (rounded to two decimal places).
Present value of $1 receivable at the end of 6 years at 5 per cent
| After | 1 yr | 2 yrs | 3yrs | 4 yrs | 5 yrs | 6 yrs |
|---|---|---|---|---|---|---|
| Present value of $1 | $0.95 | $0.90 | $0.86 | $0.82 | $0.78 | $0.75 |
| Discount factor | 0.95* | 0.90 | 0.86 | 0.82 | 0.78 | 0.75 |
NB: A Discount table is provided for IB exams - see page 89 of the IB BM Guide (syllabus)
Therefore, it is possible to calculate the present values of the yields (returns) from the previously used example using the correct discount factor from the table:
| Present value of income in year 1 | = | $30,000 | x | 0.95* | = | $28,500 |
|---|---|---|---|---|---|---|
| Present value of income in year 2 | = | $40,000 | x | 0.90 | = | $36,000 |
| Present value of income in year 3 | = | $50,000 | x | 0.86 | = | $43,000 |
| Total present value of all income | = | $107,500 |
This investment is now viable as the Total Present Value ($107,500) is greater than the cost ($100,000). The NPV, therefore, is $7,500.
Worked Example: Net present value (NPV)
Our company - Student Computers - wants a minimum return on its investment of 15%, after allowing for the time value of money. We can work out what Project B is worth in terms of today's money using the discount factors below.
| Discount rate 15% |
|---|
| Year in future | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Discount factor (f) | 0.870 | 0.756 | 0.658 | 0.572 | 0.497 |
The project has a capital cost of $700k and the net cash inflow for each year will be:
Cash inflow for year x discount factor (for year)
| Year | Cash inflow | Discount factor | Net cash inflow |
|---|---|---|---|
| 1 | 100,000 | 0.870 | 87,000 |
| 2 | 300,000 | 0.756 | 226,800 |
| 3 | 500,000 | 0.658 | 329,000 |
| 4 | 300,000 | 0.572 | 171,600 |
| 5 | 200,000 | 0.497 | 99,400 |
| Total cash inflow | $ 913,800 |
The project is worth $913.8k in today's money, but costs only $700k. This means that it has a net present value (NPV) of +$213.8k.
i.e. $913.8 - $700k = + $ 213.8k
This means that the project should bring in more money than simply investing the $700k in the bank at a rate of 15%.
Note how NPV is written as + or - , $ , number. You must give the sign (+/-) and the money unit as well as the number itself. Do not forget the thousands if they are there.
Interpretation of NPV
- NPV is positive: The project earns more than the discount rate. The project has 'passed' this test, and may be considered further.
- NPV is zero: The project earns exactly the discount rate. It may or may not be rejected.
- NPV is negative: The project earns less than the discount rate. The project will be rejected.
Benefits of Discounting/NPV
- Considers all cash flows
- Accounts for the time value of money and therefore considers the opportunity cost
- It is more scientific than the other methods
Limitations of NPV
- Complex to calculate
- Only as good as the original data. If the estimates of cost or net cash inflows are wrong, so will be the NPV
- The selection of the discount factor is crucial, but it is mostly guesswork as this rate is constantly changing
- NPV's look deceptively accurate
- Ignores all and any non-financial factors.

1 |
Average rate of returnThe average rate of return for a project gives you: |
2 |
Discounted cash flowDiscounted cash flow methods of investment appraisal |