Microeconomics

Table of Contents

1. Topic pack - Microeconomics - introduction
2. 1.1 Competitive Markets: Demand and Supply
3. 1.1 Competitive Markets: Demand and Supply - notes
4. 1.1 Competitive markets - questions
5. 1.1 Competitive markets - simulations and activities
6. 1.2 Elasticities
7. 1.2 Elasticities - notes
   1. Price elasticity of demand (PED)
   2. PED values
   3. Determinants of price elasticity
   4. Calculating PED
   5. Elasticity along a straight line demand curve
   6. Elasticity and revenue
   7. PED - primary vs manufactured
   8. PED and taxation
   9. Cross elasticity of demand
   10. XED and business decisions
   11. Income elasticity of demand
   12. YED and business decisions
   13. Price elasticity of supply
   14. Possible PES values
   15. PES - calculation
   16. Determinants of PES
   17. PES - primary vs manufactured
8. Section 1.2 Elasticities - questions
9. Section 1.2 Elasticities - simulations and activities
10. 1.3 Government intervention
11. 1.3 Government Intervention - notes
12. 1.3 Government intervention - questions
13. 1.3 Government intervention - simulations and activities
14. 1.4 Market failure
15. 1.4 Market failure - notes
16. Section 1.4 Market failure - questions
17. Section 1.4 Market failure - simulations and activities
18. 1.5 Theory of the firm
19. 1.5 Theory of the firm - notes (HL only)
20. Section 1.5 Theory of the firm - questions
21. Section 1.5 Theory of the firm - simulations and activities
22. Print View

Elasticity and revenue

Syllabus Heading: Applications of price elasticity of demand

Syllabus: Examine the role of PED for firms in making decisions regarding price changes and their effect on total revenue.

PED and business decisions - the effect of price changes on revenue

PED is important for business decision making as it determines the effect of price changes on total revenue (PxQ). When a business is considering increasing or decreasing price, it is important to know the resulting impact on demand and therefore sales revenue.

Remember that if demand for a good or service is price inelastic then an increase in price will decrease sales but increase sales revenue - can you see why? However, a price cut will increase sales but decrease sales revenue.

NB. If price elasticity is 1, then revenue does not change with a change in price since the proportionate effects on price and quantity demanded are equal.

The changes in revenue for different elasticity values are summarised in the table below.

While for completeness perfectly elastic, perfectly inelastic and unitary elastic demands are included in textbook explanations in the real world firms invariable face relatively elastic and/or relatively inelastic demands only.

Also be careful how you phrase all this it is demand that is elastic (or inelastic) not the goos. Otherwise you may end up writing about elastic cars, for example, which is just silly.                                       

Consider the following demand curves:

Unit elastic demand

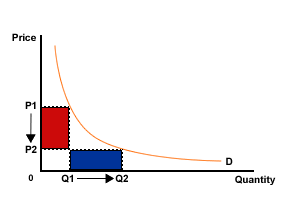
Figure 1 Unit elasticity of demand

Here the curve is a rectangular hyperbola. Thus all rectangles under the curve are equal in area and each rectangle equals total revenue (for example, the blue and red rectangles are equal). Thus, total revenue remains unchanged as price changes.

In this case it might not be worthwhile for a business to lower price as the extra demand would not bring forth any extra revenue (MR = 0), but it is highly likely that extra costs would be incurred in producing the additional output.

Elastic demand

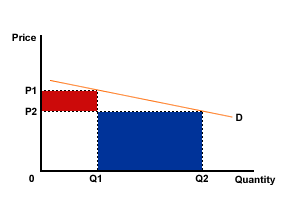
Figure 2 Elastic demand (PED greater than 1 but less than infinity)

Here a decision to reduce price would lead to an increase in total revenue. As price falls from OP1 to OP2, there is a more than proportionate rise in the quantity demanded from OQ1 to OQ2 and total revenue rises from OP1 x OQ1 to OP2 x OQ2. The fall in revenue from the lower price (the red area) is more than compensated by the rise in revenue from the extra sales (the blue area). The decision to lower price may well be sound in this case as total revenue will rise which may lead to higher profits, depending on the relationship between costs and revenue.

Conversely, a decision to raise price would lead to a fall in total revenue. A rise in price from OP2 to OP1 would cause a more than proportionate fall in demand and so reduce total revenue.

Inelastic demand

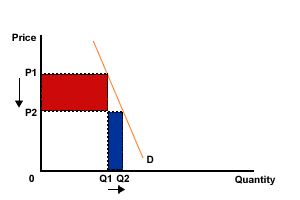
Figure 3 Inelastic demand (PED greater than 0, but less than one)

Here a decision to lower price would lead to a decrease in sales revenue. As price decreases from OP1 to OP2, there is a less than proportionate increase in demand from OQ1 to OQ2 and total revenue falls. We can see from figure 3 that the loss in revenue from the lower price (the red area) is less than the gain in revenue from the higher sales (the blue area) and so total revenue will fall.

Conversely, a decision to raise price from OP2 to OP1 would lead to a less than proportionate fall in demand from OQ2 to OQ1 and sales revenue would rise.

Thus knowledge of the PED facing a firm's product or service enables rational pricing decisions to be made.